|
<マッチ箱で作るNN#1/2>
さて、私たちの脳の働きや、
それを人工知能がどのようにモデル化したかについては、
前回お話ししました。
原理はとてもシンプルなので、
なんとなく仕組みはわかっていただけたと思います。
が、なんだか釈然としないと感じている方も
多いと思います。
僕自身もはじめてこの手の本を読んだとき、
そういう居心地の悪い気持ちになりました。
で、それはなんでだろう?どこがだろう?
といろいろ考えたんですが、
それはどうもこういうことらしいとおもいました。
脳の仕組みも、
それをモデルにした人工知能の仕組みもわかった。
でも、何かを学習するとか、問題を解くとか、
推理するとか、具体的にどうするのか、
そもそも人工知能(機械)が記憶するとか
推理するとかってどういうことなのか、
それが釈然としないのです。
自分(の脳)なら、話は簡単です。
何か問題を与えれば、脳の中で、
勝手(自動的)に答えが浮かんできます。
どう、問題を理解して整理しているか、
どうそれを脳細胞に割り振っているか、
どういう流れで答えが浮かんでくるか?
最終的にどの脳細胞が興奮していたら、
それを答えと思うんだろうか?
ふつう、我々は、そんなこと全然意識することはないです。
あらためて、整理してみようにも、
どうやって自分の脳が問題を理解して、
答えを出しているか、さっぱりわかりません。
なのに、人工知能の場合、
そういう段取りを人間がしなくてはなりません。
プログラミングの知識のある人なら、
数式(数理モデルのこと)が何か(情報)を記憶する、
推理するってことがどういう仕組みなのか、
なんとなく感覚的にわかると思いますが、
そういうことに縁遠い人には、
「機械が記憶したり推理したりすること」が、
体感的にピンとこないわけです。
脳細胞や人工知能モデルの仕組みの簡単さに比べて、
そこらあたりがあまりに共感できないために、
尺然としないんです。(少なくてもぼくはそうでした)
ということで、なんとか、人工知能がモノを覚えたり、
推理したりするってことがどういうことなのか、
数学的センスのない人にも理解でき、
あわよくば体験できる、
そんなことはできないものかと考えたのが、
本のタイトルにもあるマッチ箱を使った(人工知)脳です。
マッチ箱を脳細胞、
マッチ棒をそこに流れる(電気)信号に見立てて、
どう人工の脳が記憶したり、推理したりするか、
シミュレーションしようというモノです。
ここでは、たった4箱のマッチ箱が
「遠足のお菓子問題」
(1000円でどのくらい、
いろいろなお菓子を持っていけるか?てな問題)
を解きます。
今回と次回では、
その仕組みと実験の手順を紹介していきます。
結構、扱うマッチ棒の数が多いので、
実際やるには骨が折れるかもしれませんが、
なんとも不思議な感覚を体験できると思いますから、
是非ためしてみてください。
以下、「マッチ箱の脳」の「ニューラルネットワーク」より抜粋
●体験するNN
さて、ここでは、マッチ箱を使って、
NNの簡単な学習方法を体験していただきたいと思います。
このシミュレーションでは、
セル君が受け渡しする電気信号の量をマッチ棒で表します。
実際に自分の手でマッチ棒を動かしていきますから、
入力、出力に信号がどう伝わっていくのか、
伝わる量がどのようなルールで修正されていくかなどが、
文章を読むだけよりずっとわかりやすくなるはずです。
●マッチ箱を用意してください
というわけで、NNのモデルを
マッチ箱とマッチ棒で作ろうというのが、
この章の目的です。
ここではNNの最初のモデル、
パーセプトロンの仕組みを使うことにしましょう。
NNの章では、
セルB〜D君からセルA君に送られる
電気信号の量をどうやって調整するかについては
具体的には述べていませんが、マッチ棒のやりとりから、
そのあたりのことを説明できるかと思います。
では、マッチ箱を用意してください。
マッチ箱は4箱、マッチ棒は
200本くらい用意してください。
この4箱のマッチ箱がセルA〜D君となります。
構造は、前章で説明したモデルと同じです。
マッチ棒は信号の役目を務めます。
ちなみに、人間の脳には、
だいたい200億個の脳細胞があるといわれていますから、
とんでもない差がありますが、
こんな「小さな脳」にも、
「お菓子の買い方」をちゃんと学習させることができます。
十分に学習させた4つのマッチ箱を持っていけば、
きっと正しい買い物ができることでしょう(笑)。
□用意する道具
◆マッチ箱 4箱
◆マッチ棒 200本くらい
◆マッチ箱NNの構図を描くための紙(必要なら)
◆電卓(必要なら)
□準備
マッチ箱、マッチ棒の配置の仕方は以下のようにします。
◆マッチ箱3箱は、1番目の列に並べます。
パーセプトロンのセル君たちと、同じ並び方です。
この後列の3個の箱同士は結ばれていません。
◆残り1つのマッチ箱はその前の列に置きます。
後列のマッチ箱3個と
前のマッチ箱を結ぶ線を描いておくと、
お互いの関係がわかりやすいかもしれません。
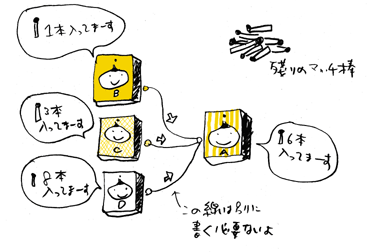
ちなみに、説明のため、
後列1〜3個のマッチ箱を
マッチ箱B、C、D、前のマッチ箱をマッチ箱Aと
呼ぶことにします。
マッチ箱の配置が終わったら、
各マッチ箱に適当な本数のマッチ棒を入れることにします。
何本でもかまわないのですが、
とりあえず、次の本数を入れるとしましょう。
◆マッチ箱B : 1本
◆マッチ箱C : 3本
◆マッチ箱D : 8本
◆マッチ箱A : 6本
残ったマッチ棒は、「山マッチ棒」として
そこらに置いておいてください。準備は以上です。
●マッチ箱、マッチ棒の役割
まず、4つのマッチ箱A〜Dの役割ですが、
これはセルA〜D君と同じです。
ちょっとおさらいしますと、
セルB〜D君は入力=インプット担当、
セルA君は出力=アウトプット担当でした。
ここでは、B〜D君には
それぞれ担当するお菓子が決まっています。
セルB君の担当はお菓子1、セルC君の担当はお菓子2、
セルD君の担当はお菓子3です。
そして、担当のお菓子を「買う」場合は興奮し、
「買わない」場合は興奮しないというルールにします。
セルB〜D君が興奮すると、A君に電気信号を送ります。
送る電気信号の量は、B〜D君それぞれ異なります。
A君に送る電気信号の量を調整することで、
NNは与えられた問題について
模範解答通りの反応ができるようになります。
そして、例題とそれに対する
模範解答を勉強をすることによって、
まだ経験していない問題についてもうまく推理して、
判断できるというのがNNの特徴でした。
●遠足のお菓子問題
さて、実際にマッチ箱NNに解いてもらう問題ですが、
ここでは、
次のような「遠足のお菓子問題」にしてみました。
――今、駄菓子屋に、お菓子1<310円>、
お菓子2<220円>、お菓子3<70円>の
3種類のお菓子が売られています。
このお菓子を買って、修学旅行に持っていこうと思います。
しかし、旅行に持っていける
お菓子の総額は500円までと決まっています。
ということは、どう考えても、
すべてのお菓子を買って持っていくわけにはいきません。
どれとどれを持っていけばいいでしょうか?
そこで、買い物アドバイザーNNの登場です。
買い物アドバイザーNNには、
「これもこれも買いたいんだけど、大丈夫かな?」
と聞くと
「規則内です、問題ありません」
か
「制限額を超えています、この買い物は違反です」
のいずれかの判断をしてくれるという機能を持たせます。
さて、お菓子の種類は3種類、
つまり買い方の場合分けは8種類しかありませんし、
判断材料は、
買ったお菓子の合計額が500円以内かどうかですから、
とても簡単な計算です。
ですから、この例の買い物に
「確かに、そんな買い物アドバイザーNNがいたら、
とても便利」
だと思う人がいたら、
そちらの方が問題あるかもしれません。
まあ、あまり実用的ではないアドバイザーですが、
この章では
自分で学習していくシステムを理解してもらうのが
目的ですから、
あえて簡単なモデルでいきたいと思います。
原理的には、このNNは、
もっとたくさんの種類の商品があり条件も複雑で、
ちょっとの暗算では不可能な、場合によっては、
計算式を立てられないような複雑な買い物でも
うまくアドバイスしてくれるはずです。
ただし、複雑な問題の場合、
マッチ箱で作った
買い物アドバイザーNNに任せるとなると、
とんでもない数のマッチ箱と
マッチ棒を持ち歩くことになります。
そしてそのマッチ棒の調整にも
かなりの根気と忍耐と時間が必要になります。
ですから、そのような場合には、
ノートブック型のパソコン上で動くNNにするべきです。
なんて、まじめに答える必要もないですね。
●模範解答を作りましょう
ということで、お菓子の種類が3つしかないので、
買い方のバリエーションも8通りしかないですし、
その買い方が正しいかどうかの判断も簡単です。
結論から言うと、
全部のお菓子を買う<合計=600円>、
お菓子1+お菓子2を買う<合計=530円>、
この2つの買い方がNGとなります。
8通りしかないので
すべての場合を調べるにしても簡単です。
すべての買い方のバリエーションが
規則に合っているかどうかは、以下のようになります。
1.お菓子1=買う お菓子2=買う お菓子3=買う は NG
2.お菓子1=買う お菓子2=買う お菓子3=買わない は NG
3.お菓子1=買う お菓子2=買わない お菓子3=買う は OK
4.お菓子1=買わない お菓子2=買う お菓子3=買う は OK
5.お菓子1=買う お菓子2=買わない お菓子3=買わない は OK
6.お菓子1=買わない お菓子2=買う お菓子3=買わない は OK
7.お菓子1=買わない お菓子2=買わない お菓子3=買う は OK
8.お菓子1=買わない お菓子2=買わない お菓子3=買わない は OK
(一応規則には合っている)
場合分けが8通りしかなく、
しかも答えがあらかじめはっきりわかっているので、
全部の場合について模範解答を用意してしまうことも
簡単なのですが、
それではマッチ箱NNの
想像力が発揮できる場がなくなってしまいますから、
つまらないですね。
ですので、上の8つから1〜5の場合を
例題として教えることにしましょう。
あとの3つの場合6〜8についてはあえて教えない。
5つの例題についての勉強から
自分で推測させることにします。
こうなると、どっちが
アドバイザーかわからなくなってしまいますが、
まあ、結構楽しい実験なのでやってみましょう。
|





