|
<考えない知能#3>
今回は、前回の「強化学習」の続きです。
マッチ箱でできた脳が、行く先々で分かれ道がある山道を、
トライアンドエラーで歩き回りながら、
ゴール(山頂)までの道を覚えていきます。
ここでは、山頂へのルートという例題になっていますが、
よくテレビなんかで見る
「ねずみは迷路を覚えられるか」的な
課題と同じだとおもってください。
以下、「マッチ箱の脳」の「ニューラルネットワーク」より抜粋
■マッチ箱強化学習
●迷い道くねくね
さて、具体的には強化学習法は
どのようにして学習していくものなのでしょうか。
大概の場合、ある場面でどうしていいか悩むということは、
つまりいくつかの選択肢があって、
どれを選んだらいいのか悩むということだと思います。
強化学習法では、各場面につき、
そういう選択肢がいくつもある。
そしてその時点では、どの選択が正しいかわからない。
そういう状況を想定して、学習を始めます。
先ほどの山登りの話を例に取って見ていきましょう。
そして、ここでもマッチ箱とマッチ棒を登場させて、
学習の過程を体験してみてもらうことにします。
――見知らぬ山道を歩いている。
目標は、山頂にたどり着くことだとしましょう。
目標に到達すれば成功、
行き止まりになってしまったら失敗とします。
□用意する道具
◆マッチ箱 8箱
◆マッチ棒 各箱4本
◆8面体サイコロ 1つ
□準備
地図は以下のように決めます。
分岐点は4つで、各分岐点では道は
左右2又に分かれています。
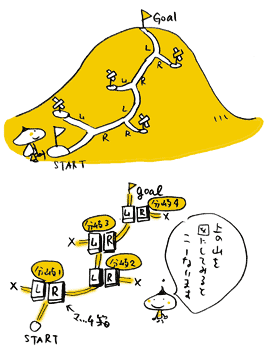
マッチ箱は、各分岐点の各道の上に
2個ずつ並べて置きます。
そして、各マッチ箱には、
最初4本ずつマッチ棒を入れておきます。
各分岐点のマッチ箱のうち、
右に置かれたマッチ箱は
右の道に行くことを進めるマッチ箱(マッチ箱R)、
左に置かれたマッチ箱は
左の道に行くことを進めるマッチ箱(マッチ箱L)です。
準備は以上です。
●右か左か……
さて、いよいよと山頂に向かっての旅のスタートです。
各分岐点で左右どちらに進むかは、
各分岐点に置かれた2つのマッチ箱の中のマッチ棒の数と、
サイコロの目の関係から決まります。
まず、サイコロを振ります。
サイコロの目が、マッチ箱Rのマッチ棒の数と同じか、
それ以下なら右方向へ進み、
それ以上だったら、左方向へ進みます。
最初、右方向マッチ箱のマッチ棒の数は4本ですから、
サイコロの目が4までだったら右へ進む、
そうでなければ左へ進むことになります。
同様に、マッチ箱Rのマッチ棒の数は2本だったら、
サイコロの目が2までだったら右に進む、
そうでなければ左に進むことになります。
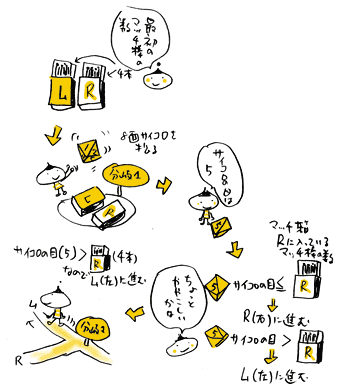
●さっそく進んでみる
まずサイコロを振ります。
サイコロの目は5だったとしましょう。
最初、どのマッチ箱にもマッチ棒は4本でしたから、
<サイコロの目>マッチ箱Rのマッチ棒の数となり、
結果、分岐点1では左方向へ進むことになりました。
図を見ていただければわかるように、
分岐点1で左方向に進むと行き止まりです。
このように、行き止まりに入ってしまったら
その回の冒険は終了です。
逆に、行き止まりに行くか、
山頂にたどり着くまでは冒険が続けられます。
●ペナルティーとご褒美
さて、冒険が終了したら、勉強タイムです。
冒険が終了するということは、行き止まりに行ったか、
山頂にたどり着いたかのいずれかです。
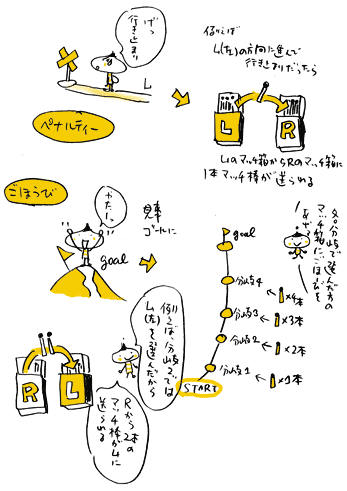
行き止まりに行ったらペナルティーを与え、
山頂にたどり着いたらご褒美を与えてやります。
まず、ペナルティーのルールです。
上の例では、分岐点1で左方向を選んだため、
行き止まりに行ってしまいました。
よって、分岐点1で左方向に進むことを進めた
マッチ箱Lにペナルティーが与えられます。
ペナルティーとして、
マッチ箱Lの中のマッチ棒1本をマッチ箱Rに渡します。
この結果、
マッチ箱Lには3本のマッチ棒、
マッチ箱Rには5本のマッチ棒となりました。
このように、
行き止まりに行かせてしまった
マッチ箱のマッチ棒が1本減らされ、
一方のマッチ箱に与えられるのがペナルティーとなります。
次にご褒美の説明です。
ご褒美はゴールにたどり着いたときだけに与えられます。
ペナルティーと同じルールとなると、
分岐点4において左の道を選ばせた
マッチ箱Lだけがご褒美を与えられそうですが、
そうではありません。
分岐点4において左の道を選ばせた功績の陰には、
分岐点3で右方向を選んだこと、
分岐点2で左方向を、分岐点1で右方向を選んだことの
手柄もあるはずです。
ですから、ご褒美の場合には
それらの選択にも分け前が与えられます。
だからといって、分岐点1で右方向を選んだ時点で、
その選択を評価することはできません。
まだその時点では結果が出ていないからです。
今は地図が最初からわかっていますから、
最初からでもご褒美をあげられますが、
地図がなかったとしたら、
それが正しい選択かどうかわかりませんからね。
ですから、山頂にたどり着いてから、
初めてそれまでの分岐点での選択に
ご褒美が与えられるのです。
これが上で言った
「一つの場面で一つの行動を取ったけれど、
その時点では、それがいいのか、
悪いのか判断ができないという場合」
に対する対処方法ということになります。
さて、ご褒美の分配ですが、
すべての分岐点での選択が同じ価値があったかというと、
これは疑問です。
この場合は、コースが単純なので、
それでも問題はないでしょうが、
一般的に最後の選択がたくさんご褒美をもらえ、
その1つ前はそれより少なく、
それより前はもっと少なくと、
だんだんと少なくなっていく方が自然なような気がします。
そこで、分岐点4では、
マッチ箱Lにご褒美としてマッチ棒4本、
分岐点3では、
マッチ箱Rにご褒美としてマッチ棒3本……
といった具合にご褒美の量を減らしていきます。
そうそう、どこからご褒美をもらうかですが、
これはペナルティーのときと同じ、
もう一方のマッチ箱からもらいます。
分岐点4ではマッチ箱Rから
4本のマッチ棒がマッチ箱Lに渡されます。
ペナルティーとご褒美のルールは以上です。
ただし、例えば4本もらおうと思っても、
相手のマッチ箱に3本以下しかない場合は、
それであきらめるしかありません。
●以上を繰り返す
さて、マッチ箱強化学習方法の学習方法は、
たったこれだけです。
これを繰り返すことで、
だんだんと正しいルートを進めるようになっていきます。
例えば、最初に分岐点1で左に進んだために、
分岐点1のマッチ箱Lのマッチ棒は
3本になってしまいました。
この結果、次にサイコロの目が
最初と同じ5であった場合でも、
サイコロの目=マッチ箱Rのマッチ棒の数となり、
今度は右方向に進むことができるようになります。
もちろん、サイコロの目が7や8だったら、
相変わらず左方向に進んでしまいますが、
ペナルティーを繰り返し与えられるうちに、
マッチ箱Lのマッチ棒は0本、
つまりマッチ箱Rのマッチ棒は8本になり、
サイコロの目がなんであれ、
必ず右方向に進むことになる。
つまり分岐点1では右方向に進むことを覚えた、
そうなるわけです。
以上が、強化学習法の大ざっぱな仕組みです。
非常に簡単な仕組みですよね。
●強化学習法の弱点
強化学習法は高度の推論、判断、記憶などという
偉そうな能力は持たないのですが、
それでも、試行錯誤を繰り返すだけで
うまく問題を解決してしまいます。
こうしたことから、
このようなボトムアップな考え方こそが、
今後のAIの正しいあり方ではないかという
意見もあります。
もちろん、まだまだ問題点も残っています。
何を成功とするか、
報酬の分配方法をどうするかなどを決め込むとなると、
結構厄介な問題となるのです。
また、実際の問題では
強化学習で必要な「試行錯誤」が
許されない場合もあります。
例えばロボットに組み込んだ場合などは、
試行錯誤を繰り返していると、
満足な学習をする前に
壊れてしまうんじゃないかなどという心配もあります。
|





