|
<マッチ箱で作るNN#2/2>

今回は、前回の続きです。
マッチ箱とマッチ棒の脳が、
いかに買い物のルールを学習していくか、
それを体験してもらうことができます。
といっても、なかなかねぇ、今はライターの時代だし、
大量のマッチ箱とマッチ棒を用意するってーのも
大変でしょう。
ってことで、今回は、助っ人の登場です。
なんと、「マッチ箱の脳」を読んでくださった
原さんという方が、頼まれもしないのに(笑)、
ブラウザ上で動くシミュレーターを作ってくださいました。
(こちらからどうぞ!)
そして、原さんのご厚意でそれをこのページに
添付させてもらえました。
だから、もうマッチ箱もマッチ棒も
用意する必要はありません!ボタン操作一つで
体感してもらえます。
前回と読み合わせて、是非いじってみてください。
(本当はマッチ棒がどう移動していったか
体験してもらえると、もっと楽しいとは思うんですが)
実は、ほぼ日でやらせてもらうと
決まったときからの悲願だったんですよね。
こうして実際に実験してもらったり、
アニメーションを見てもらいながら、
読んでもらえるというスタイルが。
こればっかりは、紙ものでは難しいですからね。
インターネットならではです。
ちなみに、原さんの実験では、
「本とマッチ箱の本数が違う結果になった。」そうです。
この現象を説明するのは、
ちとややこしいので結論からいいますと、
答え(マッチ棒の組み合わせ)は
何通りでもあるってことです。
あっていれば、それでよろしい。
そういうアバウトな世界とご了承ください。
ということで。
以下、「マッチ箱の脳」の「ニューラルネットワーク」より抜粋
●マッチ棒が興奮の合図
では、シミュレーションを始めましょう。
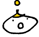
後列には3個のマッチ箱。
マッチ箱B、マッチ箱C、マッチ箱Dです。
これらは、先ほど説明した通り
それぞれ担当のお菓子が決まっています。
そして担当のお菓子を買おうとすると興奮します。
例えば、お菓子1をあなたが買おうと判断すると、
マッチ箱Bが興奮します。
もう一つのマッチ箱、マッチ箱Aは、
その買い方がOKかNGであるかの判断を担当します。
このマッチ箱Aは警告装置的性格を持っているとして、
マッチ箱Aが興奮したら「その買い方はNG!」、
興奮しなかったら「その買い方はOK」
というように解釈します。
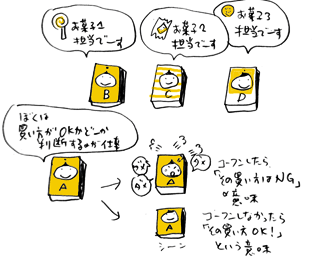
興奮したら「その買い方はOK」の方が自然じゃない?
と思われる方もいるかもしれませんが、
ここではちょっとした理由からこういう定義とします。
NNでは、出力の値(この場合はマッチ棒の数)を
どう解釈するかは設計者の自由なのです。
ところで実際のNNでは、送り出す信号や閾値に、
小数点以下の値やマイナスの値も使います。
コンピュータ上でとか数字の上でなら、
なんの問題もなく扱えるマイナス値ですが、
マッチ棒やらマッチ箱でマイナス値を表すのは
ちょっと無理ですね。
そんなこともあって、今回は、
マイナス値を使わずに済む解釈を採用しました。
さて、マッチ箱B〜Dは、
担当するお菓子を買おうと判断されると、
興奮して、おのおの決まった数のマッチ棒
(NNの章での電気信号に相当する)を
マッチ箱Aに送ります。
B〜DからAへ送るマッチ棒(信号)の数は、
その箱の中にあるマッチ棒の数と同じとします。
箱の中にマッチ棒が3本あったら、
3本のマッチ棒をマッチ箱Aに送ります。
実際、マッチ棒を送るときは、
箱の中のマッチ棒と同じ本数のマッチ棒を
「山マッチ棒」から持ってきて、
マッチ箱Aのところに渡します。
くれぐれもマッチ箱B〜Dの箱の中にある
マッチ棒を直接渡してしまわないように注意してください。
各マッチ箱の中のマッチ棒は、
何本送るかを表している記録ですから。
また、送られたマッチ棒はマッチ箱Aの横に置かれます。
これも、マッチ箱Aの中に入れてしまわないように
くれぐれも注意してください。
●ちょっとやってみましょう
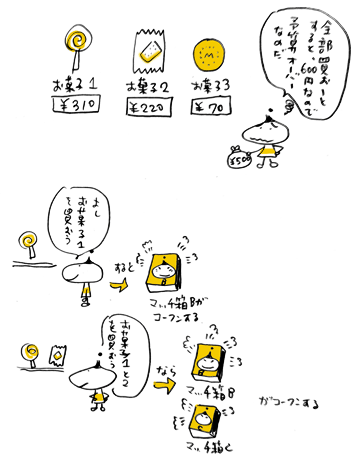
では、実際にちょっとやってみましょう。
例えば、お菓子1、2を買おうと判断した場合には、
マッチ箱B、Cが興奮しますので、
彼らの中にあるマッチ棒と同じ数の
「山マッチ棒」がマッチ箱Aに送られます。
「準備」の項で、マッチ箱Bの中には1本、
マッチ箱Cの中には
3本のマッチ棒が入っていることになっていましたから、
合計4本の「山マッチ棒」が
マッチ箱Aに送られることになります。
さて、マッチ箱Aが興奮するかどうかは
次のように判断します。マッチ箱Aに送られ、
箱の横に置かれたマッチ棒が、
マッチ箱Aの中にあるマッチの数以上だったら、
興奮する=「その買い方はNG!」。
マッチ箱Aの中にあるマッチの数以下だったら、
興奮しない=「その買い方はOK」。
そのように判断します。
そう、マッチ箱Aの中に入っている
マッチ棒の数が閾値なのです。
「準備」の項で、マッチ箱Aの中には
6本のマッチ棒が入っていましたから、
上の例で言えば、送られたマッチ棒は4本、
Aの中には6本ですから、これは興奮しない、
つまり「その買い方はOK」と
判断したということになります。
この判断は正しいでしょうか?
残念ながら、これは間違いですね。
お菓子1とお菓子2を買うと
310円+220円=530円となり、
500円までという規則に反します。
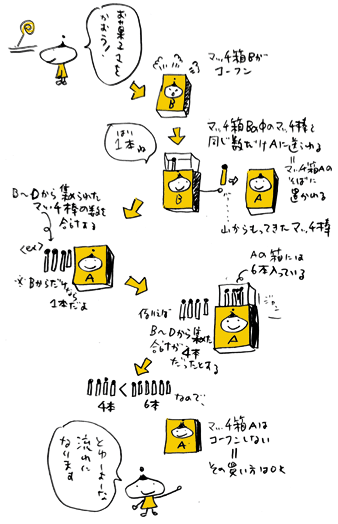
●とりあえず、マッチ箱に判断させてみる
では、正しい答えが出せるよう、学習に入りましょう。
NNにおいて勉強するとは、
送り出す信号の量と信号を受け取る
細胞の閾値の量を調整することです。
ですから、この場合では、各マッチ箱の中にある
マッチ棒の数を調整することが、
マッチ箱NNの学習ということになります。
学習の前に、まず、まだ何も勉強していない
アドバイザーが、模範解答として用意した
5つの場合について、どう判断するか見てみましょう。
1.
お菓子1=買う、お菓子2=買う、
お菓子3=買うの場合集めた
マッチ棒=1+3+8=12本>6本
(マッチ箱Aの中にあるマッチ棒の数)
よって、マッチ箱NNはNG! と判断した。
◎実際もNGなので、マッチ箱NNの判断は正しい
2.
お菓子1=買う、お菓子2=買う、
お菓子3=買わないの場合
集めたマッチ棒=1+3=4本<6本
(マッチ箱Aの中にあるマッチ棒の数)
よって、マッチ箱NNはOKと判断した。
×実際はNGなので、
マッチ箱NNの判断は間違い
3.
お菓子1=買う、お菓子2=買わない、
お菓子3=買うの場合
集めたマッチ棒=1+8=9本>6本(
マッチ箱Aの中にあるマッチ棒の数)
よって、マッチ箱NNはNG! と判断した。
×実際はOKなので、
マッチ箱NNの判断は間違い
4.
お菓子1=買わない、お菓子2=買う、
お菓子3=買うの場合
集めたマッチ棒=3+8=11本>6本
(マッチ箱Aの中にあるマッチ棒の数)
よって、マッチ箱NNはNG! と判断した。
×実際はOKなので、マッチ箱NNの判断は間違い
5.
お菓子1=買わない お菓子2=買わない
お菓子3=買わないの場合
集めたマッチ棒=0本<6本
(マッチ箱Aの中にあるマッチ棒の数)
よって、マッチ箱NNはOKと判断した。
◎実際にもOKなので、マッチ箱NNの判断は正しい
結果、2つの場合について正解、3つは間違いでした。
このマッチ箱NNの名誉のために言うと、
まだ何も勉強していない状態なので、
これは仕方がないことです。
また、逆に2つの正解も単なる偶然にすぎません。
そこで全部の模範解答通りに正解を出すように、
勉強をさせることにします。
●マッチ箱は反省し、勉強する
さて、反省して勉強させるためには、
マッチ棒を減らしたり、
増やしたりするペナルティーを与えます。
ただし、判断が正しかった場合は、
ペナルティーは与えません。
よく考えてみると、マッチ箱NNの間違いのタイプは、
次の2つしかありませんね。
◆間違いタイプ1:
正しい買い方だったのに、NGと判断してしまった。
◆間違いタイプ2:
間違った買い方だったのに、OKと判断してしまった。
タイプ1の間違い
「正しい買い方だったのに、NGと判断してしまった」
とは、マッチ箱Aが本来なら興奮してはいけないのに、
興奮してしまったということですね。
そして、マッチ箱Aが
(間違って)興奮してしまったということは、
セルB〜D君から送られたマッチ棒が
マッチ箱Aの中にあるマッチ棒の数より
多かったということでした。
これは、送られたマッチ棒の数が多すぎたか、
マッチ箱Aの中のマッチ棒が少なすぎたか、
いずれかが原因です。
そんなふうに考えていくと、
間違いタイプ1
「正しい買い方だったのに、NGと判断してしまった」
は、マッチ箱B〜Dのマッチ棒が多すぎたか、
マッチ箱Aの中のマッチ棒が
少なすぎたためだということです。
同様に、間違いタイプ2
「間違った買い方だったのに、OKと判断してしまった」
は、マッチ箱B〜Dのマッチ棒が少なすぎたか、
マッチ箱Aの中のマッチ棒が多すぎたためといえます。
この反省をもとに、多すぎたマッチ棒を減らす、
少なすぎたなら増やすという処方を取ります。
つまり、
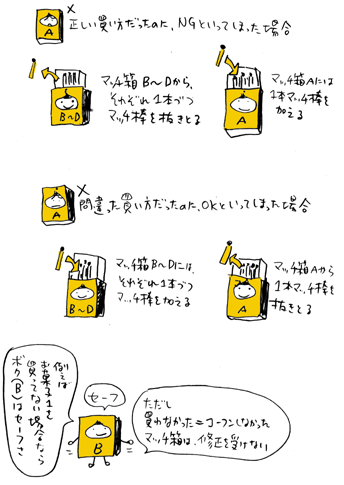
◆間違いタイプ1の間違いをしてしまったら、
マッチ箱B〜Dのマッチ棒を1本減らし、
マッチ箱Aのマッチ棒を1本増やす
◆間違いタイプ2の間違いをしてしまったら、
マッチ箱B〜Dのマッチ棒を1本増やし、
マッチ箱Aのマッチ棒を1本減らす
というマッチ棒の調整を行います。
非常に簡単ですね。
ただ、マッチ箱B〜Dについては、
1つだけルールが加わります。注意してください。
◆特別ルール:
マッチ箱B〜Dが興奮していなかった場合、
つまり、担当のお菓子を買わない場合は、
たとえ、そのとき、マッチ箱Aが間違いをしても、
マッチ棒を減らされたり、
増やしたりするペナルティーは免除される。
例えば、こういうことです。
お菓子1=買わない、お菓子2=買う、お菓子3=買う
という買い方は、実際はOKなのに、
マッチ箱AはNG! だと間違いの判断をしました。
これは、間違いタイプ1ですから、
送り出す側のマッチ棒を1本減らし、
マッチ箱Aのマッチ棒を1本増やすという
ペナルティーが与えられます。
しかし、お菓子1は買わない、
つまり、マッチ箱Bは興奮していませんから、
彼だけはルールによって
ペナルティーを免除されるということです。
その結果、この場合は、
◆マッチ箱B : ペナルティーを免除
◆マッチ箱C : マッチ棒を1本減らす
◆マッチ箱D : マッチ棒を1本減らす
◆マッチ箱A : マッチ棒を1本増やす
となるわけです。
これが基本的な修正方法になります。
●繰り返し教えてあげる
こうして、それぞれの買い方に対して、
それに対する判断が正しいか間違っているかを判断して、
間違っている場合には、その間違いのタイプに応じて、
マッチ箱の中のマッチ棒を増減させます。
マッチ箱は1回に1つの買い方についてしか
反省と修正ができません。
ですから、5つの例題について勉強させる場合には、
1つ目の例題を判断させる→
正しい判断だったかどうか判定する→
2つ目の例題を判断する→
正しい判断だったかどうか判定する→
……→
5つ目の例題を判断する→
5つ目の場合について判断して修正する。
と、順番に例題について判断させ、修正していきます。
これが1サイクルとなります。
しかし、大概の場合、
1サイクルだけの学習では十分とはなりません。
全部の場合について、模範解答通りに答えられるまで、
このサイクルを何回も繰り返します。
1つの例題(買い方)についてだけ正解を出すような
各マッチ箱のマッチ棒の数を決めるのは簡単です。
しかしすべての例題(この問題では5通り)について、
正解できるマッチ棒の組み合わせを見つけるとなると、
人間でもなかなか大変です。
さて、それはともかく、
以上のようなシンプルなルールで、
マッチをあれこれ調節していくうちに、
5つの例題について模範解答通りに
答えられるようになります。
疑っておられる方もおいでになるかもしれませんが、
原理的には、
模範解答に「矛盾」がない限り、
必ずすべての例題について模範解答通り答えられる
組み合わせを見つけられることが、
数学的に証明されていますから安心してください。
実際に行った実験で得られた、
各マッチ箱のマッチ棒数は、次のような組み合わせでした。
◆マッチ箱B : 8本
◆マッチ箱C : 6本
◆マッチ箱D : 2本
◆マッチ箱A : 11本
ちなみに、こうしてマッチ棒の数を決められた
アドバイザーNNは、教えていない残り3つの場合にも、
正しく答えらました。
●マッチ箱でもやればできる。
間違いの種類に従った
簡単なルールでマッチ棒の調節する、
たったこれだけの作業を繰り返すことで、
マッチ箱がお菓子の買い方の判断を学んでしまいます。
このマッチ箱NNでは、たくさんのマッチ箱
(入出力ユニット)を使ったり、
小数点やマイナス値が使えないなど、
コンピュータ上のシミュレーションでは
考えられない不便さがあったため、
問題を簡単にするより方法がありませんでしたが、
基本的な構造はおわかりいただけたと思います。
現在最もよく利用されている
NNにおける信号の量の調整方法はもう少し複雑ですが、
修正方法の原理はだいたいこういうことです。
原理的には、
マッチ箱NNでもマッチ箱(入出力ユニット)を
うんと増やせば、もっとたくさんのこと、
いろいろなことを覚え込ませることもできますので、
根性のある方はいろいろ試してみてください。
|





